Quantifiers, Definitions, and the Proofs of Theorems

∞

Quantifiers, Definitions, and the Proofs of Theorems

Now that quantified statements has been defined, the rules of inference can be applied to these statements to prove, or validate, mathematical theorems, or arguments.

It was mentioned in earlier sections that in scientific writing, the mathematician must avoid the situations where an ambiguous interpretation can occur, such as using an implication when a biconditional was intended. However, definitions are an exception to this rule.

Example
Consider the universe of all quadrilaterals in the plane. To try and identify what kind of quadrilateral makes a rectangle, one individual may say that, “If a quadrilateral is a rectangle, then it has four equal angles.” Another individual might identify these special quadrilaterals by saying, “If a quadrilateral has four equal angles, then it is a rectangle.”
Both individuals are making implicitly quantified statements, where the quantifier is universal.
Given the following open statements:
p(x): x is a rectangle.
q(x): x has four equal angles.
What the first individual said can be expressed as the following:
∀x [p(x) → q(x)]
And what the second individual said can be expressed as the following:
∀x [q(x) → p(x)]
Both individuals feel their implication statements identify a rectangle, but since one statement is the converse of the other, and generally the implication and its converse are not logically equivalent, then it may appear as though it is impossible for both to be true.
However, the problem is the intention that was not considered. In this situation, each individual was using an implication with the meaning of a biconditional, where they both intended but did not directly state that ∀x [p(x) ↔ q(x)], which is read as, “A quadrilateral is a rectangle if and only if the quadrilateral has four equal angles.”

Example
Consider the universe of all integers. The even integers can be distinguished by a certain property, and so an even integer is defined as the following:
For every integer n, n is even if it is divisible by 2.
(Where “divisible by 2” means exactly divisible by 2 with no remainder.)
Given the open statements:
p(n): n is an even integer.
q(n): n is divisible by 2.
It appears that the definition of an even integer can be written symbolically as ∀n [q(n) → p(n)], because the definition is an implication. However, what was stated is again not intended. The intention is for the reader to interpret the definition as biconditional, where ∀n [q(n) ↔ p(n)], read as, “For every integer n, n is even if and only if n is divisible by 2.”
Note that the open statement, “n is divisible by 2,” can also be written as the open statement, “n = 2k for some integer k.” The words, “For some integer k,” can be misleading that, since the open statement is using an existential quantifier, the open statement may be thought of as just a statement. However, it is still an open statement, because n remains a free variable.

Therefore, it is only in definitions that an implication can be (mis)read and correctly interpreted as a biconditional. Then, in definitions, the wording “if” can also be read as “if and only if.”

Method of Exhaustion
Suppose a universe consists of only 13 integers 2, 4, 6, …, 24, 26. Then the following statement can be establish as valid:

For all n (in the universe), n can be written as the sum of at most three perfect squares.

The following provides a case-by-case verification that shows the given quantified statement is a valid argument, where this valid argument can be referred to as a theorem:

This exhaustive listing is an example of a proof using the technique called method of exhaustion. This method is reasonable when dealing with a small-sized universe. Even if the universe is slightly larger, a computer program can be written to check all of the individual cases.

Definition of Theorem
Theorem will be referred to as a true mathematical statement. Sometimes the term theorem is used only to describe major results that have varied consequences. These consequences that follow from a theorem are referred to as corollaries.

The above example is a good starting point to examine the proof of a quantified statement. Unfortunately, a great number of mathematical statements and theorems often deal with universes that make the method of exhaustion useless. For example, the method of exhaustion cannot be used if the universe was of all real numbers. Instead, the following rule is used:

The Rule of Universal Specification
If p(x) is an open statement for some universe, and if the statement ∀x p(x) is true, then p(a) is true for every a in the universe.

This rule indicates that the truth of an open statement for one particular value of variable(s) follows from the more general truth of the universally quantified statement for the entire universe.

Example
Consider the universe of all people and the following open statements:
m(x): x is a mathematics professor.
c(x): x has studied calculus.
Consider the following argument:
All mathematics professors have studied calculus.
Leona is a mathematics professor.
Therefore, Leona has studied calculus.
Let l denote the particular human Leona in the universe. Then the argument can be rewritten in symbolic form:

The two statements above the line are the premises of the argument, and the statement c(l) below the line is its conclusion. This is similar to regular arguments, but now a quantified statement is in the premise. Just like with validating regular arguments, the premises are all assumed to be true, and it must be established that the conclusion is also true under these circumstances.
To validate the argument:

Note that the statements m(l) and m(l) → c(l) are not quantified statements. They are the same type of statements studied earlier, and so the rules of inference can be applied to them.
The Rule of Universal Specification can be used to take a universally quantified premise and deduce to it an ordinary statement that is not quantified. This statement, m(l) → c(l), is one specific true instance of the universally quantified true premise ∀x [m(x) → c(x)].

Example
Consider the universe of all triangles in the plane and the following open statements:
p(t): t has two sides of equal length.
q(t): t is an isosceles triangle. (two sides of equal length)
r(t): t has two angles of equal measure.
Suppose there is a triangle XYZ denoted as c such that no two of its angles are of equal measure. Then the argument can be stated as the following:
In triangle XYZ, there is no pair of angles of equal measure.
If a triangle has two sides of equal length, then it is an isosceles.
If a triangle is isosceles, then it has two angles of equal measure.
Therefore, triangle XYZ has no two sides of equal length.
This argument can be expressed in symbolic form:

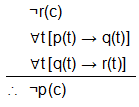
This argument is then validated:

Example
Consider the universe made up of the entire student body at a particular college. Let m denote the one specific student named Mary Gusberti. Consider the following open statements:
j(x): x is a junior.
s(x): x is a senior.
p(x): x is enrolled in a physical education class.
Consider the following argument:
No junior or senior is enrolled in a physical education class.
Mary Gusberti is enrolled in a physical education class.
Therefore, Mary Gusberti is not a senior.
This argument can be expressed in symbolic form:

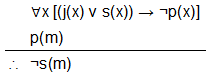
To validate the argument:

Modus Ponens and Modus Tollens for Quantifiers
The following is the valid argument of Modus Ponens which is valid when used after the Rule of Universal Specification with a fixed universe that contains a specific element c, where p(x),q(x) are both open statements defined for this universe:

Additionally, the following is the valid argument of Modus Tollens which is valid when used after the Rule of Universal Specification with a fixed universe that contains a specific element c, where p(x),q(x) are both open statements defined for this universe:

Note that, just like Modus Ponens and Modus Tollens for ordinary statements, the fallacy of using [∀x (p(x) → q(x)) ᴧ q( c)] → p(c ) and [∀x (p(x) → q(x)) ᴧ ¬p(c )] → ¬q(c ) will be errors, because these are invalid arguments.

Arbitrary Value c
Although the above examples involved premises that were universally quantified statements, there was never any time a universally quantified statement appeared in the conclusion. Since many theorems in mathematics have the form of a universally quantified statement, to remedy this situation, the following is considered:

Start with a given universe and the open statement p(x). To establish the truth of the statement ∀x p(x), the truth of p(c ) for every element c in the universe must be established. However, if the universe has many elements, such as the universe of all positive integers, the task of validating the truth of each p( c) becomes difficult, if not impossible. Instead, to prove p( c) is true for all c in the universe, it is done using the case where c denotes a specific but arbitrarily chosen element from the universe.

Let the open statement p(x) have the form q(x) → r(x), where q(x),r(x) are open statements. Assume the truth of q(c ) is an additional premise and then try to deduce the truth of r( c) by using definitions, axioms, previously proven theorems, and logical principles. When g(c ) is false, the implication g( c) → r( c) is true, regardless of the truth value of r(c ).

The reason that the element c in the universe must be arbitrary, or generic, is to make sure that c is applicable for all the other elements in the universe. For example, if the universe consisted of all integers, r cannot be chosen by just selecting c as 4, or by selecting c as an even integer. In general, no assumptions should be made about the choice of c unless those assumptions are valid for all the other elements in the universe. The word generic is applied to c, because it indicates that the choice of c must share all of the common characteristics of the elements in the given universe.

The principle that was described in the above three paragraphs is named and summarized as the following:

The Rule of Universal Generalization
If an open statement p(x) is proven to be true when x is replaced by any arbitrarily chosen element c in the universe, then the universally quantified statement ∀x p(x) is true. This rule can be extended beyond just one variable.

Example
Let p(x),q(x),r(x) be open statements that are defined for a given universe and consider the following argument:

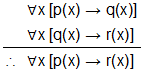
To validate this argument:

Although the specific but arbitrarily chosen element c has no special or distinguishing properties, it still shares all of the common features of every other element in the universe, and so the Rule of Universal Generalization can be used.

*Example
Consider the following argument:

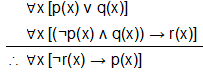
To validate this argument:

img14 *not completed*

Proofs of Theorems
Universally quantified statements and the rules of inference can be used to formalize and prove a variety of arguments and theorems. When this is done, it can appear that the validation of some rather short argument requires a lot of steps, because validation needs to be done meticulously, including all the steps and reasons.

Example
Given the following definition:
Let n be an integer. This n is even if n is divisible by 2, where there exists an integer r so that n = 2r. If n is not even, then n is odd such that there exists an integer s where n = 2s + 1.
To prove for all integers k and l, if k,l are both odd, then k + l is even:
1. Since k and l are odd, by definition of an odd integer, k and l can be written as k = 2a + 1 and l = 2b + 1 for some integers a,b.
2. Then by Commutative Law of Addition, Associative Law of Addition, and the Distributive Law of Multiplication over Addition, k + l = (2a + 1) + (2b + 1) = 2(a + b + 1).
3. Since a,b are integers, then a + b + 1 = c is an integer. Then by the definition of an even number, 2c = k + l is even.

Note that, the first step of the proof chose k and l in an arbitrary manner, and so by the Rule of Universal Generalization, the result obtained is true for all odd integers.

Additionally, this proof implicitly used the Rule of Universal Specification twice (since there were two variables k,l) in the first step of the proof. It used the definition that if n is an odd integer, then n = 2r + 1 for some integer r. The integer k is a specific but arbitrarily chosen odd integer, therefore k was written as k = 2a + 1 and l was written as l = 2b + 1 for some integers a,b.

Note that k and l use different variables a,b, because it may be the case that k does not equal l.

Example
Consider the following open statement for the universe of integers:
If n is an integer, then n² = n.
This open statement can be expressed in symbolic form as ∀n [n² = n].
If n = 0, or n = 1, the statement would be true. However, it cannot be concluded that n² = n for every integer n. The Rule of Universal Generalization does not apply here. If n = 2, the statement would be false, and this one counterexample is enough to say that the given statement is false. However, since n = 0 and n = 1 makes the statement true, then that is enough to make the statement ∃n [n² = n] true.

Method of Contradiction versus Method of Contraposition
A contradiction can be obtained by deriving the negation of a known fact, which is not the hypothesis that is trying to be proven.

Let p(m),q(m) be two open statements defined for a universe. Consider a theorem of the form ∀m [p(m) → q(m)]. If this theorem is proven using the contrapositive method, then the logically equivalent statement ∀m [¬q(m) → ¬p(m)] is proven. To prove this, assume the truth of ¬q(m) for any specific by arbitrarily chosen element m in the universe, and show that it leads to the truth of ¬p(m).

If this theorem is proven using the method of contradiction, then the statement ∀m [p(m) → q(m)] is assumed false. To show that the statement is false is showing that p(m) → q(m) is false for at least one element m from the universe, where ∃m ¬q(m) is true, making p(m) true and q(m) false. Then the truth of p(m) and ¬q(m) are used to derive a contradiction of the form p(m) ᴧ ¬p(m).

Therefore, using the method of contraposition assumes a truth value of ¬q(m) to result in the truth of ¬p(m). Using the method of contradiction assumes a truth value for p(m) and ¬q(m) to result in a contradiction statement to use the Proof by Contradiction rule.

The following example uses the method of contradiction for the previous example:

Example
Given the following definition:
Let n be an integer. This n is even if n is divisible by 2, where there exists an integer r so that n = 2r. If n is not even, then n is odd such that there exists an integer s where n = 2s + 1.
To prove the theorem that if m is an even integer, then m + 7 is odd:
1. Assume that m is even. Then by the definition of even integers, m = 2b for some integer b. Then m = 2b, m + 7 = 2b + 7 = 2b + 6 + 1 = 2(b + 3) + 1. Since b + 3 is an integer, m + 7 is odd.
2. Suppose m + 7 is not odd but even. Then m + 7 = 2a for some integer a and so m = 2a - 7 = 2a - 8 + 1 = 2(b - 4) + 1, where b - 4 is an integer. Then m is odd.
Note that Step 1 and Step 2 use the statement ∀m [p(m) → q(m)]. Since this is logically equivalent to ∀m [¬q(m) → ¬p(m)], the statement ∀m [¬q(m) → ¬p(m)] will now be considered.
3. Assume m and m + 7 are even. Then m + 7 implies that m + 7 = 2c for some integer c. As a result, m = 2c - 7 = 2c - 8 + 1 = 2(c - 4) + 1 with c - 4 an integer. Then m is odd. This is a contradiction, because m started as assumed to be even but deduced to odd. This is based on the false assumption that m + 7 is even, and so since this assumption is false, its negation is true, which means m + 7 is really odd.

The following example uses the method of contraposition:

Example
To prove that all positive real numbers x,y, if the product xy exceeds 25, then x > 5 or y > 5.
Consider the negation of the conclusion, where 0 < x ≤ 5 and 0 < y ≤ 5. Under these circumstances, it is found that:
0 = (0)(0) < (x)(y) ≤ (5)(5) = 25, and so the product xy does not exceed 25, which makes the conclusion false from a false hypothesis, creating a true statement. Since the contrapositive is logically equivalent to the implication (the original argument), this completes the proof.

PDF reference: 137

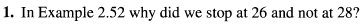
Because more than three perfect squares are needed to sum to up to 28.

a) Let p(x),q(x) denote the following open statements:

p(x): The real number x is an integer.
q(x): x is a rational number.

The argument is written in the following tabular form:

where π is an element in the universe.

To find the missing conclusion, validate the argument:

Therefore, ¬p(π): The real number π is not an integer.

a) For ∃x [p(x) ᴠ q(x)] to be true, there must exist an element c from the universe such that p(c ) ᴠ q(c ) is true. Therefore, at least one of the statements p(c ),q(c ) must be true, and so one of the statements ∃x p(x), ∃x q(x) is true, making the statement ∃x p(x) ᴠ ∃x q(x) true. Therefore, ∃x [p(x) ᴠ q(x)] => ∃x p(x) ᴠ ∃x q(x).

b) For ∀x [p(x) ᴧ q(x)] to be true, then for any c from the universe, p( c) ᴧ q( c) must be true. Then both p( c) and q( c) are true for any element c in the universe, so ∀x p(x) and ∀x q(x) are both true, making the statement ∀x p(x) ᴧ ∀x q(x) true. Therefore, ∀x [p(x) ᴧ q(x)] => ∀x p(x) ᴧ ∀x q(x).

a) The contrapositive to this statement is logically equivalent. Suppose k,l are both even integers, and so for some integers a,b, let k = 2a and l = 2b. Then by Associative Law for Multiplication and Commutative Law for Multiplication, kl = (2a)(2b) = 2(2ab). Since a,b are integers, 2ab = c is an integer. Then kl = 2c is an even product. Since this contrapositive argument is valid, it confirms that the original statement holds.

Suppose n is even and n² is odd. By definition of an integer, for some integer a, let n = 2a. Then n² = (2a)² = 4a² = 2(2a²). Since a is an integer, 2a² = c is an integer. When n² = 2c is even. This produces a contradiction by falsely assuming n² to be odd, when later it is deduced that n² is not odd, but even. This confirms the proof.

Let p(m,n),q(m,n),r(m,n) denote the following open statements:

p(m,n): x and y are positive integers.
q(m,n): x and y are perfect squares.
r(m,n): x + y is a perfect square.

Argument: ∀m,n [(p(m,n) ᴧ q(m,n)) → r(m,n)]
Negation: ¬[∀m,n [(p(m,n) ᴧ q(m,n)) → r(m,n)]]
∃m,n ¬[(p(m,n) ᴧ q(m,n)) → r(m,n)]
∃m,n ¬[¬(p(m,n) ᴧ q(m,n)) ᴠ r(m,n)]
∃m,n [¬¬(p(m,n) ᴧ q(m,n)) ᴧ ¬r(m,n)]
∃m,n [(p(m,n) ᴧ q(m,n)) ᴧ ¬r(m,n)]

Therefore, to disprove that for all positive integer m,n, if m,n are perfect squares, then m + n is a perfect square, then it must be found that there exists some integers m,n such that m,n are positive perfect squares but their sum m + n is not equal to a perfect square.

Let m = 1, n = 4. Then m + n = 1 + 4 = 5. This counterexample is enough to conclude the invalidity of the original argument.

harrlson-wells liked this
lawsofemotion posted this

Algebra, Linear Algebra, Geometry, Vector Geometry, Trigonometry, Pre-Calculus, and Single-Variable Calculus

Quantifiers, Definitions, and the Proofs of Theorems