Algebra, Linear Algebra, Geometry, Vector Geometry, Trigonometry, Pre-Calculus, and Single-Variable Calculus

The Use of Quantifiers

In Section 2.1, it was mentioned that sentences involving a variable, such as x, are not statements (because they are neither true or false) unless the value for that variable is defined. For example, the sentence, “The number x + 2 is an even number,” is neither true or false unless the value of x is known. If the choices for x are restricted to all integers, then the sentence becomes a false statement when an odd integer is substituted for x, or the sentence becomes a true statement when an even integer is substituted for x. This type of sentence is referred to as an open statement.

Open Statements and Quantifiers
A declarative sentence is an open statement if it has the following three characteristics:

1. The sentence contains one or more variables.
2. The sentence is not a statement.
3. The sentence becomes a statement when the variables contained inside it are replaced by certain, allowable choices.

For example, the sentence, “The number x + 2 is an even integer,” is an open statement containing one variable x. In regards to the third characteristic, the variable’s choices are restricted to integers (because it says the number is an integer). These allowable choices create what is called the universe, or the universe of discourse, for the open statement. The universe contains the choices to consider, or allow, for the variable(s) to be set to in an open statement.

The notation p(x) (or g(x), r(x), etc.) is used to denote an open statement. Therefore, if p(x) denotes the open statement, “The number x + 2 is an even integer,” then ¬p(x) denotes the open statement, “The number x + 2 is not an even integer.”

The notation q(x,y) is used to denote open statements with two variables. For example, q(x,y) can denote the open statement, “The numbers y + 2, x - y, and x + 2y are even integers.” In this case, there are more than one occurrence of each of the variables x,y. It is understood that, when a substitution is made for one occurrence of a variable, that same substitution is made for all other occurrences of that variable.

The following demonstrates an example of the above open statements defined earlier with some replacements for the variables x,y:

p(5): The number 7 (5 + 2) is an even integer. (false)
¬p(7): The number 9 (7 + 2) is not an even integer. (true)
q(4,2): The numbers 4 (2 + 2), 2 (4 - 2), and 8 (4 + (2)(2)) are even integers. (true)

Note that, p(7) and ¬q(4,2) are false statements, and ¬p(5) is a true statement.

From this observation for p(x) and q(x,y), some substitutions result in true statements and some substitutions result in false statements. Therefore, in general, the following are two true statements:

1. For some x, p(x).
2. For some x,y, q(x,y).

Note that, the statements, “For some x, ¬p(x),” and, “For some x,y, ¬q(x,y),” are also true statements. Therefore, the statement, “For some x, ¬p(x),” is not the negation of the statement, “For some x, p(x).” Similarly, the statement, “For some x,y, ¬q(x,y),” is not the negation of the statement, “For some x,y, q(x,y).”

The phrases, “For some x,” and, “For some x,y,” are said to quantify the open statements p(x) and q(x,y), respectively. Many definitions and theorems in mathematics involve statements that are quantified open statements.

There are two types of quantifiers, which are called the existential quantifier and the universal quantifier.

Both of the two true statements above use the existential quantifier “For some x.” This can also be expressed as, “For at least one x,” or, “There exists an x such that.” The existential quantifier is denoted as ∃x, and so the statement, “For some x, p(x),” becomes ∃x p(x) in symbolic form. Similarly, the statement, “For some x,y, q(x,y),” becomes ∃x ∃y q(x,y), or ∃x,y q(x,y).

The universal quantifier is denoted as ∀x, read as, “For every x,” or, “For any x,” or, “For all x.” Therefore, “For every x,y,” “For any x,y,”, or “For all x,y,” is denoted as ∀x ∀y, or ∀x,y. Using the above true statement ∃x p(x): “For some x, p(x)”, if it was changed to the universal quantifier ∀x p(x), the statement would then become false, because the universe is all integers and ∀x symbolizes all integers, including odd integers. However, if r(x): “2x is an even integer” uses the same universe of all integers, then ∀x r(x) would be a true statement. Additionally, ∃x r(x) is also a true statement, whereas ∀x ¬r(x) and ∃x ¬r(x) are both false statements.

The variable x in the open statements p(x) and r(x) is called a free variable of the open statement. As x varies over the universe for an open statement, the truth value of the statement can vary. For example, with p(x), p(5) is a false statement while p(6) is a true statement. However, with r(x), it is a true statement for every x taken from the universe of all integers.

For the open statement p(x), the statement ∃x p(x) has a fixed truth value of true. Therefore, the variable x is a bound variable, where x is bounded by the existential quantifier ∃. Similarly, for the statements ∀x r(x) and ∀x ¬r(x), the variable x is bounded by the universal quantifier ∀. With the statement ∃x,y q(x,y), the two free variables x,y are each bounded by the existential quantifier ∃.

The following example uses the idea of quantifiers with logical connectives:

Example
Consider the universe containing all real numbers. The following are open statements p(x),q(x),r(x),s(x):
p(x): x ≥ 0
q(x): x² ≥ 0
r(x): x² - 3x - 4 = 0
s(x): x² - 3 > 0
Factoring r(x) gives (x - 4)(x + 1) = 0. Therefore, the following statement is true:
∃x [p(x) ᴧ r(x)]
“There exists a real number x such that x ≥ 0 and (x - 4)(x + 1) = 0.”
This statement is true, because, if x = 4, it is inside the universe and both p(4) and r(4) are true statements.
Consider the following implication:
∀x [p(x) → q(x)]
“For every real number x, if x ≥ 0, then x² ≥ 0.”
If x equals a negative number, then p(x) is false while q(x) is true, making the implication true. Additionally, ∀x q(x) will always be true, because any number square is zero or positive. This automatically makes the statement ∀x [p(x) → q(x)] true no matter the truth value of p(x).
Additionally, ∃x [p(x) → q(x)] is a true statement.
Consider the following implication:
∀x [q(x) → s(x)]
“For every real number x, if x² ≥ 0, then x² - 3 > 0.”
s(x) can be rewritten as “x² > 3.” This statement is false, because it was shown that ∀x q(x) is a true statement, and so the hypothesis will always have a truth value of 1, however, there are some real numbers x such that q(x) is true but s(x) is false, such as x = 1, making q(1) true and s(1) false, which causes the implication to be false. Since the quantifier is universal, the statement is false, because not all real numbers x satisfy this statement.
Consider the following disjunctive:
∀x [r(x) ᴠ s(x)]
“For every real number x, (x - 4)(x + 1) = 0 or x² > 3.”
This statement is false, because there are counterexamples found to show that not every real number x satisfies this statement. However, if the quantifier was changed to the existential quantifier, then the statement becomes true.

Note that p(x) can stand for a compound open statement with logical connectives. For example p(x) can denote the compound statement q(x) ᴧ r(x), etc.

Logical Implication and Quantifiers
Let p(x) denote any open statement in the free variable x with a nonempty universe, where the universe contains at least one element. Then, if ∀x p(x) is a true statement, then ∃x p(x) is also a true statement.

∀x p(x) => ∃x p(x)

The implication ∀x p(x) → ∃x p(x) is a logical implication, where the statement ∃x p(x) is true whenever the statement ∀x p(x) is true. However, ∃x p(x) does not logically imply ∀x p(x), where ∃x p(x) ≠> ∀x p(x).

Implicit Quantification
The following example demonstrates that an open statement may not always contain explicit quantification:

Example
Consider the universe of all real numbers and the following sentences:
1. If a number is rational, then it is a real number.
2. If x is rational, then x is real.
These two sentences convey the same information, however it can be difficult to determine whether the sentences are statements or open statements. The second sentence contains a variable, yet it is unsure whether this sentence uses quantifiers, because neither sentence contains the explicit quantifiers. However, notice that the indefinite article “a” is used in the first sentence. This is the only clue to indicate the sentence is a quantified statement using the universal quantifier. In this case, the universal quantifier was implicit rather than explicit.
Let p(x),q(x) denote the following open statements:
p(x): x is a rational number
q(x): x is a real number
The fact must be recognized that both of the above sentences give an informal way of expressing the quantified statement ∀x [p(x) → q(x)].

Example
For the universe of all triangles in the plane, the sentence, “An equilateral triangle has three angles of 60°, and conversely,” also demonstrates implicit quantification. The indefinite article “an” is used to indicate the universal quantifier, and so if e(t) denotes the open statement, “Triangle t is equilateral,” and a(t) denotes the open statement, “Triangle t has three angles of 60°,” then the given sentence can be written in the explicit quantified symbol form ∀t [e(t) ↔ a(t)].

Example
The following is a very common trigonometry identity:
sin²x + cos²x = 1
This identity contains no explicit quantification or indefinite articles to indicate the quantifier. Instead, the reader must understand or be told that this identity is defined for all real number x. When this is understood or specified, then this identity can be expressed by the explicit quantified statement ∀x [sin²x + cos²x = 1].

Example
Consider the universe for all positive integers ℤ⁺ and the sentence, “The integer 41 is equal to the sum of two perfect squares.”
Not every single positive integer can satisfy this open statement, and so the quantifier this time is existential, which can be written in symbolic form as ∃x,y [41 = x² + y²].

The following example demonstrates that the truth value of a quantified statement may sometimes depend on the universe:

Example
Consider the open statement p(x): x² ≥ 1.
If the universe consists of all positive integers, then the quantified statement ∀x p(x) is true, because the universe contains 1, 2, 3, …, +∞.
However, if the universe consists of all positive real numbers, then the quantified statement ∀x p(x) is then false, because the universe contains also fractions that are between 0 and 1, which provide counterexamples.
Yet, for either universe, the quantified statement ∃x p(x) is true.

Truth Values for Quantified Statements
Given the statement ∃x p(x), it is a true statement when there exists an a in the universe such that the statement p(a) is true. The statement ∃x p(x) is false when, for every a in the universe, the statement p(a) is false.

Given the statement ∀x p(x), it is a true statement when, for every a in the universe, the statement p(a) is true. The statement ∀x p(x) is false when there exists an a in the universe such that the statement p(a) is false.

Given the statement ∃x ¬p(x), it is a true statement when there exists an a in the universe such that the statement p(a) is false. The statement ∃x ¬p(x) is false when, for every a in the universe, the statement p(a) is true.

Given the statement ∀x ¬p(x), it is a true statement when, for every a in the universe, the statement p(a) is false. The statement ∀x p(x) is false when there exists an a in the universe such that the statement p(a) is true.

Logical Equivalence, Logical Implication, and Quantifiers
Let p(x),g(x) be open statements defined for some universe. Then the open statements p(x),q(x) are logically equivalent, or equivalent, denoted as ∀x [p(x) <=> q(x)], when the biconditional p(a) ↔ q(a) is a tautology for all a in the universe.

Let p(x),g(x) be open statements defined for some universe. Then the open statement p(x) logically implies q(x), denoted as ∀x [p(x) => q(x)], when the implication p(a) → q(a) is a tautology, or valid argument, for all a in the universe.

For example, for the universe of all triangles in the plane, let p(x),q(x) denote the following open statements:

p(x): x is equiangular. (equal angles)
q(x): x is equilateral. (equal sides)

Then, for every particular triangle a (replacement for x), p(a) ↔ q(a) is true, where p(a) <=> q(a) for every triangle in the plane. Therefore, ∀x [p(x) <=> q(x)].

Note that, ∀x [p(x) <=> q(x)] ↔ [∀x [p(x) => q(x)] ᴧ ∀x [q(x) => p(x)]].

Implication, Contrapositive, Converse, and Inverse for Quantified Statements
For the open statements p(x),q(x) defined for some universe, the contrapositive for the universally quantified statement ∀x [p(x) → q(x)] is [¬q(x) → ¬p(x)]

The converse for the universally quantified statement ∀x [p(x) → q(x)] is ∀x [q(x) → p(x)].

The inverse for the universally quantified statement ∀x [p(x) → q(x)] is ∀x [¬p(x) → ¬q(x)].

Example
For the universe of all quadrilaterals in the plane, let s(x) and e(x) denote the following open statements:
s(x): x is a square.
e(x): x is a equilateral.
The statement ∀x [s(x) → e(x)] is a true statement, and it is logically equivalent to its contrapositive ∀x [¬e(x) → ¬s(x)].
For each replacement a in the universe, [s(a) → e(a)] <=> [¬e(a) → ¬s(a)]. Therefore, ∀x [s(x) → e(x)] <=> ∀x [¬e(x) → ¬s(x)].
The statement ∀x [e(x) → s(x)] is the converse of the true statement ∀x [s(x) → e(x)], and so ∀x [e(x) → s(x)] is a false statement. However, the contrapositive of the converse statement ∀x [¬s(x) → ¬e(x)], or the inverse of ∀x [s(x) → e(x)], is logically equivalent to the converse ∀x [e(x) → s(x)], and so ∀x [¬s(x) → ¬e(x)] is also false. Therefore, ∀x [e(x) → s(x)] <=> ∀x [¬s(x) → ¬e(x)].

Example
Let p(x),q(x) denote the following open statements, where the universe consists of all real numbers:
p(x): |x| > 3
q(x): x > 3
The statement ∀x [p(x) → q(x)] is false, because if x = -5, then p(-5) is true yet q(-5) is false, making the implication false. That makes the contrapositive false, and the converse and inverse true statements.

Example
Now consider the addition of another open statement r(x):
p(x): |x| > 3
q(x): x > 3
r(x): x < -3
Then ∀x [p(x) → (r(x) ᴠ q(x))] is true and the converse ∀x [(r(x) ᴠ q(x)) → p(x))] is also true. If they are both true, then the contrapositive ∀x [¬(r(x) ᴠ q(x)) → ¬p(x))] and the inverse ∀x [¬p(x) → ¬(r(x) ᴠ q(x))] are also true.

Example
Consider the universe of all integers and the following open statements denoted as r(x), s(x):
r(x): 2x + 1 = 5
s(x): x² = 9
The statement ∃x [r(x) ᴧ s(x)] is false, because there doesn’t exist any integer a such that both 2a + 1 = 5 and a² = 9 are true. However, there does exist an integer b (2) such that 2b + 1 = 5 and an integer c (± 3) such that c² = 9. Therefore, the existential quantifier ∃x does not distribute over the logical connective ᴧ, where ∃x [r(x) ᴧ s(x)] <≠> [∃x r(x) ᴧ ∃x s(x)], and so [∃x r(x) ᴧ ∃x s(x)] → ∃x [r(x) ᴧ s(x)] is not a tautology and therefore not a logical implication either.
However, the converse of [∃x r(x) ᴧ ∃x s(x)] → ∃x [r(x) ᴧ s(x)], which is ∃x [r(x) ᴧ s(x)] → [∃x r(x) ᴧ ∃x s(x)] is in fact a tautology, and therefore a logical implication. When the hypothesis ∃x [r(x) ᴧ s(x)] is true, there is at least one element a in the universe such that r(x) ᴧ s(x) is true. By the Rule of Conjunctive Simplification, two separate two statements ∃x r(x) and ∃x s(x) are formed. Then, by the Rule of Conjunction, ∃x r(x) ᴧ ∃x s(x) are formed. Therefore, ∃x [r(x) ᴧ s(x)] => [∃x r(x) ᴧ ∃x s(x)].

Rules of Inference and Laws of Logic for Quantifiers
For some universe and any open statements p(x),q(x),r(x) in the variable x, the following are logical equivalences and logical implications for quantified statements in one variable:

1. Distributive Law Existential Implication for ᴧ

∃x [p(x) ᴧ q(x)] => [∃x p(x) ᴧ ∃x q(x)]

2. Distributive Law Existential Equivalence for ᴠ

∃x [p(x) ᴠ q(x)] <=> [∃x p(x) ᴠ ∃x q(x)]

3. Distributive Law Universal Equivalence for ᴧ

∀x [p(x) ᴧ q(x)] <=> [∀x p(x) ᴧ ∀x q(x)]

4. Distributive Law Universal Implication for ᴠ

∀x [p(x) ᴠ q(x)] => [∀x p(x) ᴠ ∀x q(x)]

5. Associative Law Universal Equivalence for ᴧ

∀x [p(x) ᴧ (q(x) ᴧ r(x))] <=> ∀x [(p(x) ᴧ q(x)) ᴧ r(x)]

6. Biconditional Tautology Existential Equivalence

∃x [p(x) → q(x)] <=> ∃x [¬p(x) ᴠ q(x)]

7. Double Negation Law Equivalence

∀x ¬¬p(x) <=> ∀x p(x)
∃x ¬¬p(x) <=> ∃x p(x)

8. DeMorgan’s Law Equivalence

∀x ¬[p(x) ᴧ q(x)] <=> ∀x [¬p(x) ᴠ ¬q(x)]
∀x ¬[p(x) ᴠ q(x)] <=> ∀x [¬p(x) ᴧ ¬q(x)]
∃x ¬[p(x) ᴧ q(x)] <=> ∃x [¬p(x) ᴠ ¬q(x)]
∃x ¬[p(x) ᴠ q(x)] <=> ∃x [¬p(x) ᴧ ¬q(x)]

Negation and Quantified Statements
Consider the statement ∀x p(x). Its negation is ¬[∀x p(x)], which can be read as, “It is not the case that for every x, p(x) holds.” When ¬[∀x p(x)] is true, then ∀x p(x) is false, and for some a in the universe, ¬p(a) is true, which makes ∃x ¬p(x) true. Therefore, the statement ¬[∀x p(x)] is true if and only if the statement ∃x ¬p(x) is true. Since this biconditional is a tautology, ¬[∀x p(x)] <=> ∃x ¬p(x).

Therefore, the rules for negating statements with one quantifier are the following:

1. ¬[∀x p(x)] <=> ∃x ¬p(x)
2. ¬[∃x p(x)] <=> ∀x ¬p(x)
3. ¬[∀x ¬p(x)] <=> ∃x ¬¬p(x) <=> ∃x p(x)
4. ¬[∃x ¬p(x)] <=> ∀x ¬¬p(x) <=> ∀x p(x)

Example
Consider the universe of all integers, where p(x),q(x) denote the following open statements:
p(x): x is odd.
q(x): x² - 1 is even.
Then the following is a true statement:
∀x [p(x) → q(x)]
“For every integer x, if x is odd, then x² - 1 is even.”
To negate this statement:
¬[∀x (p(x) → q(x))]
<=> ∃x [¬(p(x) → q(x))]               (Rule of Negation)
<=> ∃x [¬(¬p(x) ᴠ q(x))]               (Biconditional Tautology Existential                                                                         Equivalence)
<=> ∃x [¬¬p(x) ᴧ ¬q(x)]                (DeMorgan’s Law Equivalence)
<=> ∃x [p(x) ᴧ ¬q(x)]                    (Double Negation Law Equivalence)
Therefore, the negation can be read as, “There exists an integer x such that x is odd and x² - 1 is odd.” This statement is false.

Example
Consider the universe of all integers, where r(x),s(x) denote the following open statements:
r(x): 2x + 1 = 5
s(x): x² = 9
The quantified statement ∃x [r(x) ᴧ s(x)] is false, because it asserts that there exists an integer x such that 2x + 1 = 5 and x² = 9 are both true, which is not true, because no such x exists.
Consider its negation ¬[∃x (r(x) ᴧ s(x))]:
¬[∃x (r(x) ᴧ s(x))]
<=> ∀x ¬[r(x) ᴧ s(x)]                      (Negation Law)
<=> ∀x [¬r(x) ᴠ ¬s(x)]                    (DeMorgan’s Law Equivalence)
This negated statement ∀x [¬r(x) ᴠ ¬s(x)] is true.

Logical Equivalence for Quantified Statements in Two Variables

Example
Consider the universe that consists of all real numbers and two real variables x,y. The commutative law for the addition of real numbers is expressed as the following:
∀x ∀y (x + y = y + x)
It can also be expressed as the following:
∀y ∀x (x + y = y + x)
For the case of commutative law for the multiplication of real numbers, it can be expressed as the following two statements:
∀x ∀y (xy = yx)
∀y ∀x (xy = yx)

The above example produces the general equivalence for quantified statements with two variables:

Given p(x,y) is an open statement in two variables x,y, then:
∀x ∀y p(x,y) <=> ∀y ∀x p(x,y)

Example
Consider the universe of all real numbers, the associative law for the addition of real numbers x,y,z is the following:
x + (y + z) = (x + y) + z
Using universal quantifiers, it can be expressed in the following two ways:
∀x ∀y ∀z [x + (y + z) = (x + y) + z]
∀x,y,z [x + (y + z) = (x + y) + z]
In fact, there are 3! = 6 ways to arrange the three universal quantifiers ∀x,∀y,∀z. All six of these arrangements are logically equivalent to each other.

Additionally, in regards to the usage of only existential quantifiers in two or more variables, the ordering of the quantifiers does not matter.

However, the following example demonstrates that order does matter when working with both existential quantifiers and universal quantifiers:

Example
Consider the universe of all integers and let p(x,y) denote the open statement, “x + y = 17.”
The statement ∀x ∃y p(x,y) is read as, “For all integers x, there exists an integer y such that x + y = 17. This statement is true, because once any x is selected from the universe, the integer y = 17 - x does exist in the universe as well.
The statement ∃y ∀x p(x,y) is read as, "There exists an integer y such that, for every integer x, x + y = 17.” This statement is false, because, once the integer y is selected, there can only be one fixed value of x to satisfy x + y = 17.
If the statement ∃y ∀x p(x,y) were true, then every integer x would equal 17 - y, for some fixed value y. This would imply that all integers are equal.

The above example results in the general result that ∀x ∃y p(x,y) and ∃y ∀x p(x,y) are not logically equivalent.

Importance of Logical Translation
Translating mathematical statements, such as definitions or theorems, into symbolic form is helpful for the following two reasons:

1. The symbolic form of the statements need more care and precision about the meaning of each statement and the order for each quantifier.
2. After translating the statement into symbolic form, the rules of inference and laws of logic are easier to apply when determining negation, or the contrapositive, etc.

PDF reference: 121

For a), q(1): 1 + 1 is odd.
Therefore, it is a false statement.

For b), ¬p(3): 3 > 3
Therefore, it is a false statement.

For c), p(7): 7 ≤ 3 (false), q(7): 7 + 1 is odd (false)
Therefore, p(7) ᴠ q(7) is a false statement.

For d), p(3): 3 ≤ 3 (true), q(4): 4 + 1 is odd (true)
Therefore, p(3) ᴧ q(4) is a true statement.

For e), p(-4): -4 ≤ 3 (true), q(-3): -3 + 1 is odd (false)
p(-4) ᴠ q(-3) is a true statement.
Therefore, ¬[p(-4) ᴠ q(-3)] is a false statement.

For f), ¬p(-4): -4 > 3 (false), ¬q(-3): -3 + 1 is even (true)
Therefore, ¬p(-4) ᴧ ¬q(-3) is a false statement.

For a), p(0): 0² = 2(0) (true)

For b), p(1): 1² = 2(1) (false)

For c), p(2): 2² = 2(2) (true)

For d), p(-2): (-2)² = 2(-2) (false)

For e), ∃x p(x) (true)

For f), ∀x p(x) (false)

a)
i), ∃x q(x)
ii), ∃x [p(x) ᴧ q(x)]
iii), ∀x [q(x) → ¬t(x)]
iv), ∀x [q(x) ᴧ ¬t(x)]
v), ∃x [q(x) ᴧ t(x)]
vi), ∀x [[q(x) ᴧ r(x)] → s(x)]

b)
i) true
ii) true
iii) false, let x = 10
iv) false, let x = 10
v), true
vi) true

c)
i) If an integer x is a perfect square, then x is even.
ii) If an integer x is divisible by 4, then x is even.
iii) If an integer x is divisible by 4. then x is also divisible by 5.
iv) There exists an integer x such that x is divisible by 4, but x is not a perfect square.

d)
False: i) let x = 9
False: iii) let x = 20

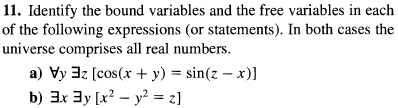
a) bounded variables: y,z
free variables: x

b) bounded variables: x,y
free variables: z

a) Let p(x,y),q(x,y) denote the following the open statements:

p(x,y): x² > y²
q(x,y) x > y

∃x,y [p(x,y) ᴧ ¬q(x,y)]: There exists real numbers x,y such that x² > y² but x ≤ y.

Therefore, since the proposed negation matches the negation of the quantified statement, the proposed negation is correct.

b) Let p(x,y),q(x,y) denote the following the open statements:

p(x,y): x and y are rational.
q(x,y): x + y is rational.

∀x,y [p(x,y) → q(x,y)]: For every real numbers x,y, if x and y are rational, then x + y is rational.

Therefore, since the proposed negation does not match the negation of the quantified statement, the proposed negation is incorrect.

d) Let p(x,y),q(x,y) denote the following the open statements:

p(x,y): x and y are odd.
q(x,y): xy is odd.

∀x,y [p(x,y) → ¬q(x,y)]: For every integer x,y, if x and y are odd, then xy is even.

Therefore, since the proposed negation does not match the negation of the quantified statement, the proposed negation is incorrect.

a)

b)

c)

d)

a) True
b) False, because the universe is nonzero integers.
c) False, this assumes all integers are equal.
d) True, the system of equations is consistent for a solution of integers.
e) False, the system of equations is consistent, yet the solution is not integers.

a) ∀x ∃y [x + y = y + x = 0]
b) ∃x ∃y [xy = yx = x]
c) ∀ x ≠ 0 ∃y [ab = ba = 1]
d) Part c) changes, since the set of integers does not contain fractions.