Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations
Problems based on Lagrange's method of multipliers
Examples
Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations: Examples
1.4.b. Problems based on Lagrange's method of multipliers
Example
1.4b(1): Solve x (y-z) p + y (z - x) q=z (x − y).

Example
1.4b(2): Solve (mz - ny) p + (nx − lz) q = ly - mx.
Solution:
Given: (mz - ny) p + (nx - lz) q = ly - mx

Example
1.4b(3) : Sove (3z-4y) p + (4x-2z) q 2y-3x.

Example 1.4b(4) Find the general
solution of


Example
1.4b(5) Solve (x2 - yz) p + (y2 − zx) q = (z2
− xy).
Solution:
Given: (x2 - yz) p + (y2 - zx) q = (z2 − xy)

Note: The author wishes to thank
Dr. B. Jothiram, formerly Asst. Prof. and HOD Maths, Govt. College of Engg.,
Salem, for having drawn his attention to this elegant method of getting one of
the independent solutions.
Example
1.4b(6): Solve (x2 + y2+ yz) p + (x2
+ y2 − xz) q = z(x + y).
-
Solution: Given: (x2 + y2+
yz) p + (x2 + y2 − xz) q = z(x + y).
This equation is of the form P p +
Q q = R

Example
1.4b(7): Solve (y2 + z2) p- xyq+xz = 0
Solution:
Given: (y2+z2) p-xyq+xzx= 0
This equation is of the form Pp+Qq
= R

Example
1.4b(8): Solve (y2
+ z) p- y(x2 +z)q = z(x2 –y2)
Solution:
This equation is of the form P p + Qq=
R
where P = X x (y2+ z), Q
= y (x2 + z), R = z ( x2 - y2).
The Lagrange's subsidiary equations
are
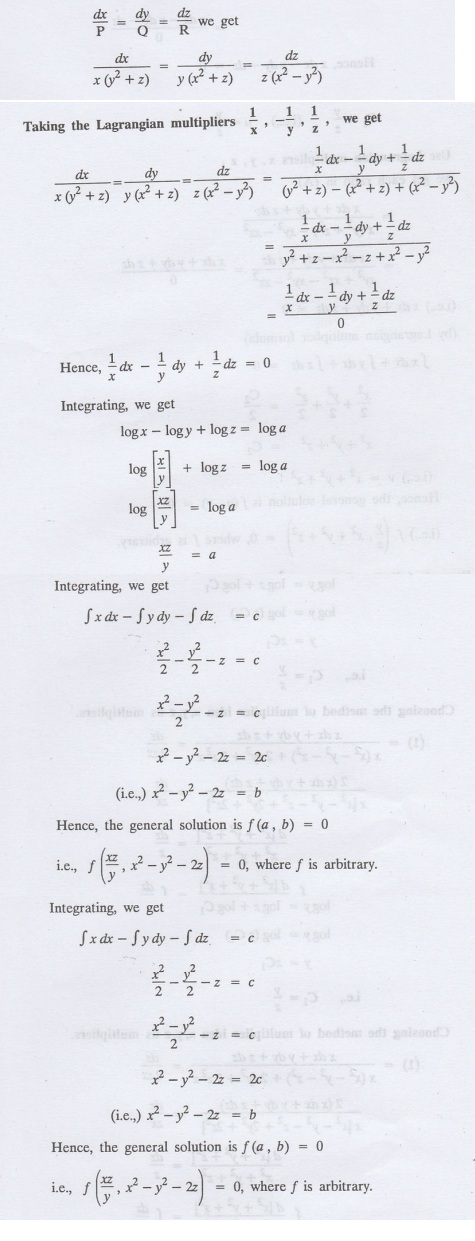
Example
1.4b(9): Solve the equation: (x2 - y2 - z2) p+
2 xyq = 2 zx
Solution:
Given: (x2 - y2 - z2) p + 2xyq = 2zx
This equation is of the form
Pp+Qq=R
The Lagrange's subsidiary equations
are

Example 1.4b(10) : Solve (z2-
2yz-y2) p + (xy + zx) q = xy - zx
Solution
:
Given: (z2- 2yz-y2) p + (xy + zx) q = xy - zx
This equation is of the form Pp+Qq
R where
P = x2-2yz-y2,
Q = xy + zx, R=xy − zx
The Lagrange's subsidiary equations
are

Example
1.4b(11): Solve (y + z) p + (z+x) q = x + y.
Solution:
Given
(y + z) p + (z+x) q = x+y
This equation is of the form
Pp+Qq=R
y+z, Q = z+x, R = x + y
The Lagrange's subsidiary equations
are

Example
1.4b(12): Solve (y-xz) p + (yz - x) q = (x + y) (x − y)
Sol.
Given: (y-xz) p + (yz − x) q = (x + y) (x − y)
This equation is of the form
Pp+Qq=R
where P=(y-xz), Q = yz -x, R= (x +
y) (x − y)

Example
1.4b(13): Solve (y-z) p − (2x + y) q = 2x + z.
Solution:
Given: (y-z)p (2x+y) q = 2x + z
This equation is of the form Pp+Qq
= R
where Py-z, Q = − (2x + y), R =
2x+z
The Lagrange's subsidiary equations
are,

Example
1.4b(14): Show that the integral surface of the equation 2y (z-3) p + (2x-z) q
= y (2x-3) that passes through the circle x2+ y2 = 2x,
z=0 is x2+y-2-2x+4z = 0.
Solution
:
Given: 2y (z - 3) p + (2x-z) q = y
(2x − 3)
This equation is of the form Pp +
Qq = R
where P = 2y (z 3), Q = 2xz, R = y
(2x-3)
The Lagrange's subsidiary equations
are

substitute for a and b from (2) and
(3) in (9), we get
x2 + y2-z2
- 2x + 4z = 0 which is the equation of the required integral surface.
Transforms And Partial Differential Equations: UNIT I: Partial Differential Equations : Tag: : Examples - Problems based on Lagrange's method of multipliers
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
